6021. Mega Inversions

The n² upper bound for any sorting algorithm is easy to obtain: just take two elements that are misplaced with respect to each other and swap them. Conrad conceived an algorithm that proceeds by taking not two, but three misplaced elements. That is, take three elements a_i > a_j > a_k with i < j < k and place them in order a_k, a_j, a_i. Now if for the original algorithm the steps are bounded by the maximum number of inversions n (n – 1 ) / 2, Conrad is at his wits' end as to the upper bound for such triples in a given sequence. He asks you to write a program that counts the number of such triples.

Input. The first line is the length of the sequence n (1 ≤ n ≤ 10⁵). The next line contains the integer sequence a₁, a₂, ..., a_n (1 ≤ a_i ≤ n).

Output. Print the number of inverted triples.

Sample input	Sample output
4 3 3 2 1	2

SOLUTION

data structures – Fenwick tree

Algorithm analysis

In cells pref[i], for each value of a_i, count the number of elements to the left and strictly greater than a_i. Then, for each a_i, count in suff[i] the number of elements to the right and strictly less than a_i.

The required number of triples is

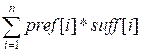
The product pref[i] * suff[i] corresponds to the number of required triples with a_i in the middle.

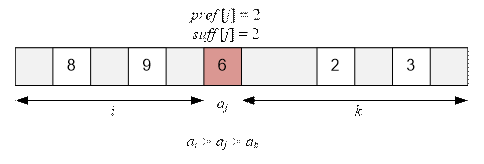
· pref[j] = 2, since to the left of a_j = 6 there are two number greater than 6: 8 and 9.

· suff[j] = 2, since to the right of a_j = 6 there are two number less than 6: 2 and 3.

There are pref[j] * suff[j] = 2 * 2 = 4 inverted triplets, in which a_j = 6 is in the middle: (8, 6, 2), (8, 6, 3), (9, 6, 2), (9, 6, 3).

Let’s take a closer look at how to build the pref[i] array. Let’s create an array b of size n, initially set its elements to zero. Simulate its processing with the Fenwick tree. At each iteration make an operation b[a[i]]++. To find out the amount of numbers greater than a[i] at the i-th iteration, compute the sum b[a[i] + 1] + b[a[i] + 2] + … + b[n]. It equals to the sum of all numbers in the array b minus the sum of b[0] + b[1] + … + b[a[i]]. The sum of all numbers in array b at the i-th iteration equals to the number of iterations i, since at each iteration we increased one of the elements b by one. In this case

pref[i] = i – (b[0] + b[1] + … + b[a[i]])

While computing the suffixes, we also simulate the operation of array b by adding b[a[i]]++ at each iteration. In this case, we consider the numbers of the array a from right to left: a_n, a_n-1, …, a₁. Then the number of elements to the right and strictly less than a_i is equal to b[0] + b[1] + … + b[a[i] – 1], which is suf[i].

Example

Consider the next test case:

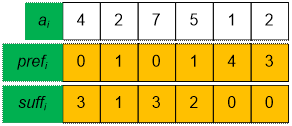
The number of required triples is

0 * 3 + 1 * 1 + 0 * 3 + 1 * 2 + 4 * 0 + 3 * 0 = 3

Consider for example, how to count the number of inversions a_i > a_j > a_k, where a_j = 5. Their number is pref[4] * suff[4] = 1 * 2 = 2.

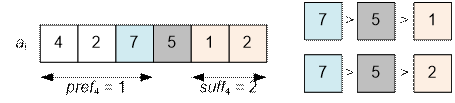
Consider the process of computing the array pref.

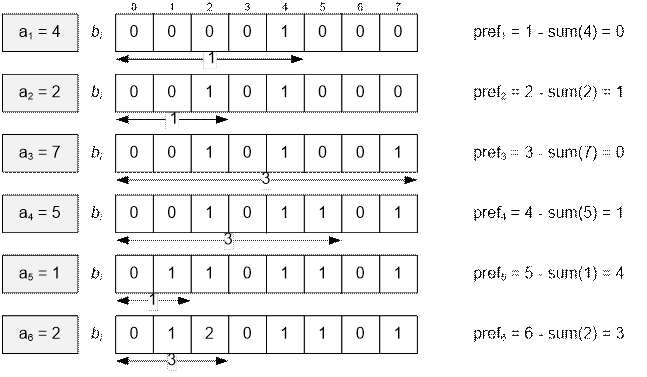
Algorithm realization

Declare the global arrays.

#define MAX 100010

int Fenwick[MAX], a[MAX], pref[MAX];

Compute the sum b[0] + b[1] + … + b[i].

int Summma0_i(int i)

{

int result = 0;

for (; i >= 0; i = (i & (i + 1)) - 1)

result += Fenwick[i];

return result;

}

Increase b[i] by one.

void IncElement(int i)

{

for (; i < MAX; i = (i | (i+1)))

Fenwick[i]++;

}

The main part of the program. Read the input data.

scanf("%d", &n);

for(i = 1; i <= n; ++i)

scanf("%d", &a[i]);

For each value of a_i, count the number of elements to the left and strictly greater than a_i. Store this value in pref[i].

for(i = 1; i <= n; i++)

{

IncElement(a[i]);

pref[i] = i - Summma0_i(a[i]);

}

Move from right to left along the array a. Compute the result according to the formula given in the problem analysis.

memset(Fenwick,0,sizeof(Fenwick));

for(i = n; i >= 1; i--)

{

IncElement(a[i]);

res += 1LL * pref[i] * Summma0_i(a[i] - 1);

}

Print the answer.

printf("%lld\n",res);

Java realization

import java.util.*;

public class Main

{

static int Fenwick[], a[], pref[];

final static int MAX = 100001;

static int Summma0_i(int i)

{

int result = 0;

for (; i >= 0; i = (i & (i + 1)) - 1)

result += Fenwick[i];

return result;

}

static void IncElement(int i)

{

for (; i < MAX; i = (i | (i+1)))

Fenwick[i]++;

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

a = new int[n+1];

pref = new int[n+1];

Fenwick = new int[MAX];

for(int i = 1; i <= n; i++)

a[i] = con.nextInt();

for(int i = 1; i <= n; i++)

{

IncElement(a[i]);

pref[i] = i - Summma0_i(a[i]);

}

Fenwick = new int[MAX];

long res = 0;

for(int i = n; i >= 1; i--)

{

IncElement(a[i]);

res += 1L * pref[i] * Summma0_i(a[i] - 1);

}

System.out.println(res);

con.close();

}

}